Heap Data Structure: A Guide

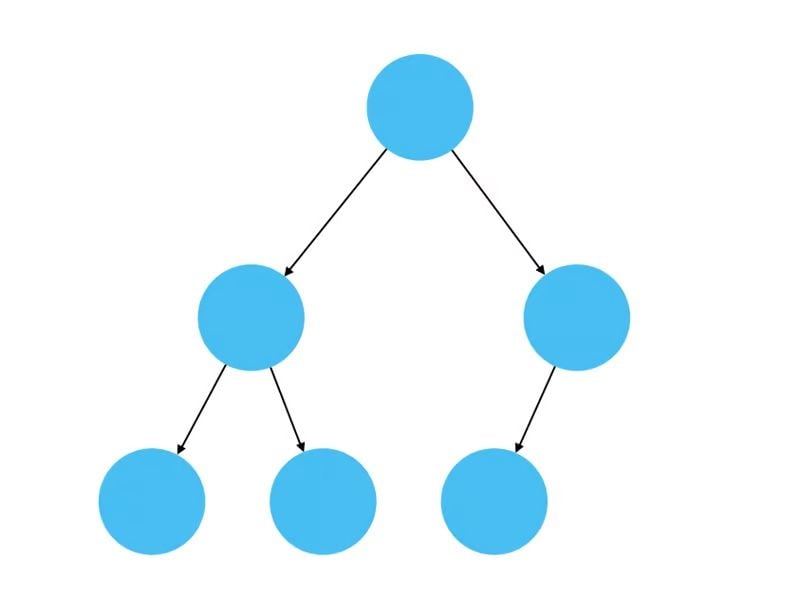
A heap is a data structure that can be represented by a complete binary tree. A complete binary tree is full up until the penultimate level, with nodes being filled from left to right on the last level. 

Below is an example of a heap.

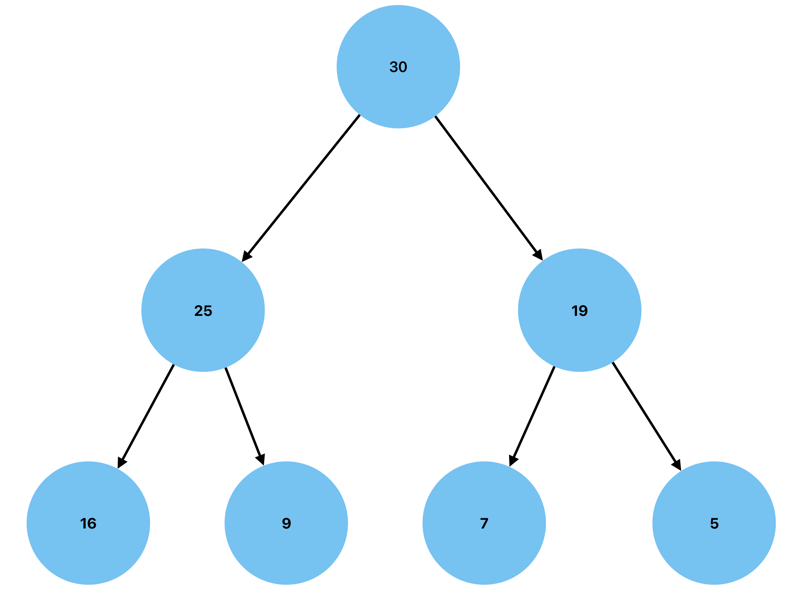
There are two types of heaps, namely a Max Heap and a Min Heap.

2 Types of Heap Data Structures

Max Heap

A heap is considered to be a Max Heap when the children nodes have values that are less than or equal to the value of the parent node. Below is a visual representation of a Max Heap.

Heaps can also be represented as arrays. Here is the same Max Heap as an array:

Min Heap

A heap is considered to be a Min Heap when the children nodes have values that are greater than or equal to the value of the parent node.

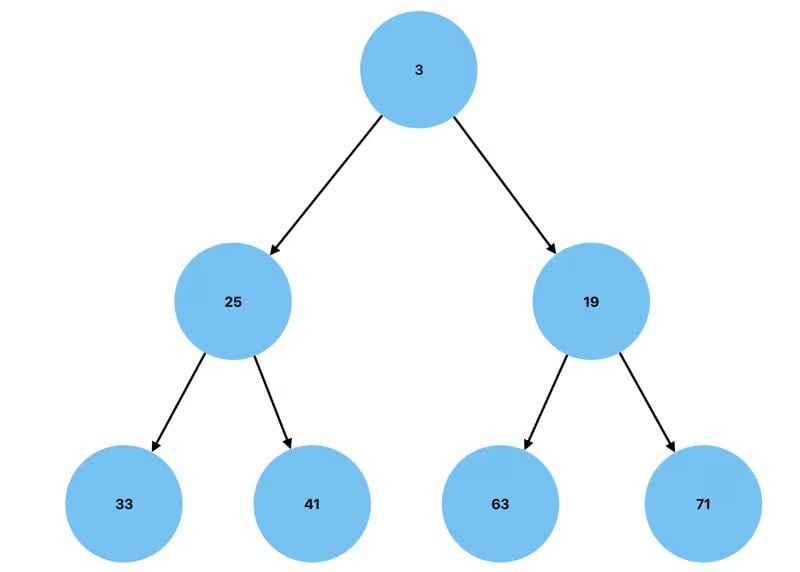
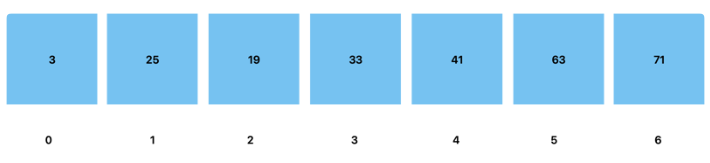
Here is a visual representation of the same Min Heap as an array:

It’s worth noting that heaps are weakly ordered and that the heap must be adjusted whenever a node is added or deleted.

Since we don’t know beforehand the number of nodes that a heap will have, heaps can be implemented in JavaScript using an arraylist. In order to manipulate a heap, we will need to take the indices of the nodes into consideration. Below is the Min Heap we used earlier, this time showing the index positions of each node.

We can use the index position of a node to calculate the indices of the children and parents. To find the children of a node, we use 2i+1 and 2i+2, where i is the index of the parent node. This can be done in JavaScript with the following code:

  leftChild = (index) => {
    return index * 2 + 1;
  };

  rightChild = (index) => {
    return index * 2 + 2;
  };

To find the parent, we use ⌊(i-1)/2⌋, where i is the index of the child. This can be done in JavaScript using the following code:

  parent = (index) => {
    return Math.floor((index - 1) / 2);
  };

More on Data ScienceBinary Search Implementation in Python: A Tutorial

5 Heap Data Structure Functions to Know

Now, we will take a look at some common heap functions. These functions will make use of the following constructor which gives the value of a node and the length of the heap.

  constructor() {
    this.data = [];
    this.length = 0;
  }

1. peak()

This function is used to return the value of the root of a heap. The peak function will return the minimum value of a Min Heap and the maximum value of a Max Heap.

   peak = () => {
    return this.data[0];
  }

2. heapifyUp()

This function compares a child node to its parent node, swapping the two if they don’t meet the conditions of the heap. In the case of a Min Heap, as shown in the code snippet below, the child and parent will be swapped if and only if the value of the parent node is greater than the value of the child node.

  heapifyUp = (index) => {
    if (index === 0) {
      return;
    }

    const parentNode = this.parent(index);
    const parentValue = this.data[parentNode];
    const childValue = this.data[index];

    if (parentValue > childValue) {
      this.data[index] = parentValue;
      this.data[parentNode] = childValue;
      this.heapifyUp(parentNode);
    }
  };

This function will be useful in insertion operations.

3. heapifyDown()

This function is used to compare the values of the children nodes, swapping one of the children with the parent node if the heap condition is not met. In the case of a Min Heap, the child with the lesser value will swap positions with the parent node if the child's value is less than that of the parent node.

  heapifyDown = (index) => {
    const leftIndex = this.leftChild(index);
    const rightIndex = this.rightChild(index);

    //check if there are children in heap
    if (index >= this.length || leftIndex >= this.length) {
      return;
    }

    const leftValue = this.data[leftIndex];
    const rightValue = this.data[rightIndex];
    const parentValue = this.data[index];

    if (leftValue > rightValue && parentValue > rightValue) {
      this.data[index] = rightValue;
      this.data[rightIndex] = parentValue;
      this.heapifyDown(rightIndex);
    } else if (rightValue > leftValue && parentValue > leftValue) {
      this.data[index] = leftValue;
      this.data[leftIndex] = parentValue;
      this.heapifyDown(leftIndex);
    }
  };
}

This function will be useful in deletion operations.

4. insert()

To add or insert a new node to a heap, said node must be added to the end of the heap.

We then compare the value of the new node with that of the parent node. In the case of a Min Heap, if the new node is less than the parent, we swap the positions of the two nodes within the heap.

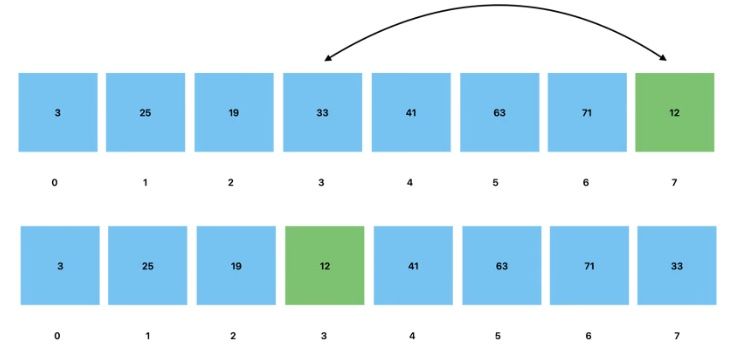
We then repeat the process, comparing the value of the node with its new parent, until it is positioned correctly. In the case of a Min Heap, the value of the new node must be less than that of the parent node.

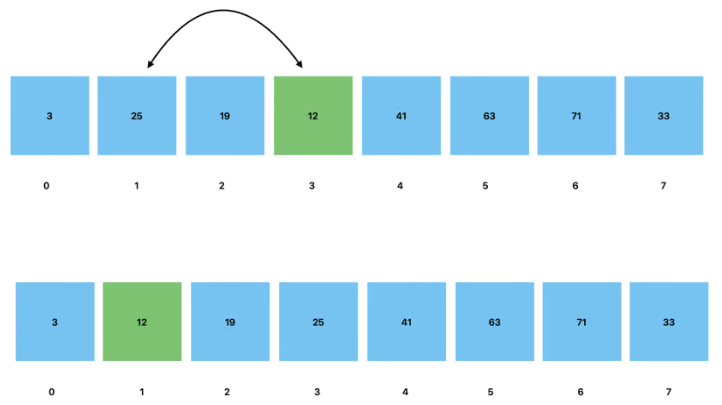
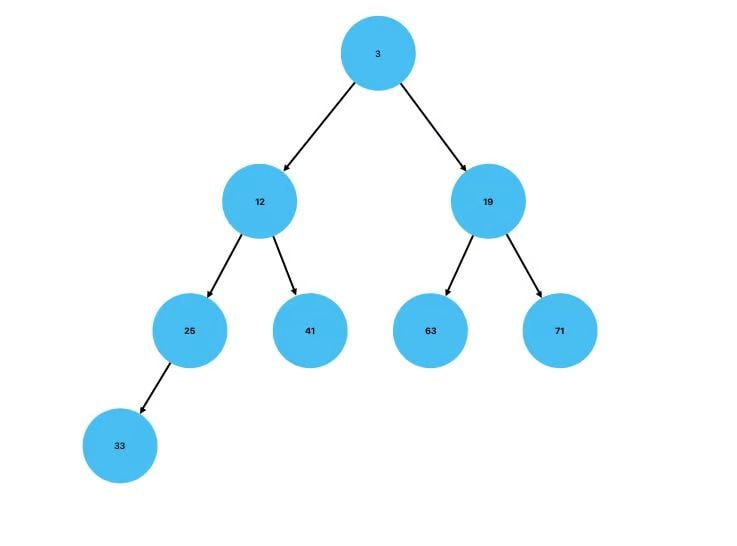
Here is the same heap represented as a tree:

The insert function can be implemented in JavaScript with the following code, taking advantage of heapifyUp() to bubble up the heap:

 insert(value) {
    this.data[this.length] = value;
    this.heapifyUp(this.length);
    this.length++;
  }

5. delete()

The root is the node that is removed when a delete operation is performed on a heap.

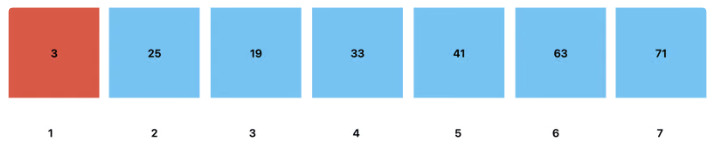
To do this, the root node is swapped with the last node of the heap. This node is then removed from the heap, with its value being stored elsewhere if so desired.

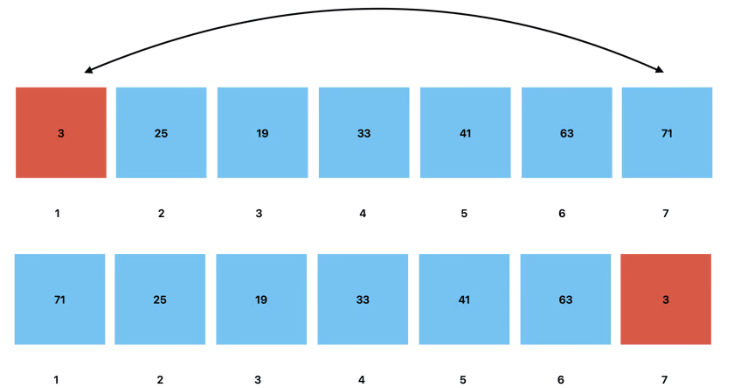
We then compare the new root with its children. In the case of a Min Heap, if the value of the root is greater than the values of either of the children nodes, we swap the root with the child with the lesser value.

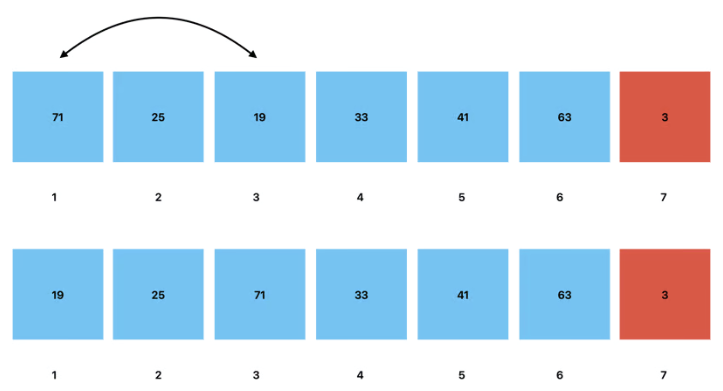
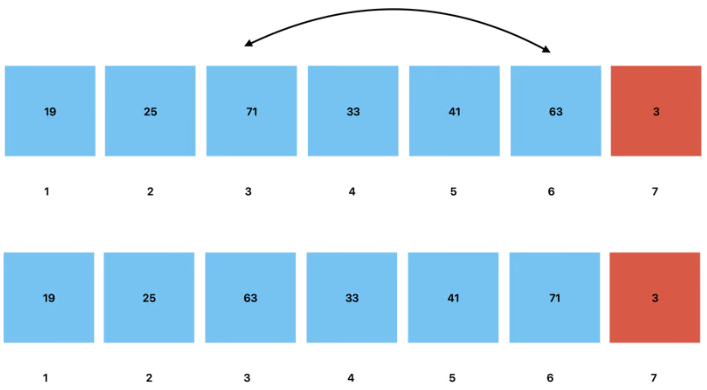
We repeat this process of comparing and swapping until the tree meets the requirements of a Min Heap. That is to say, that each child node has a value greater than that of its parent node.

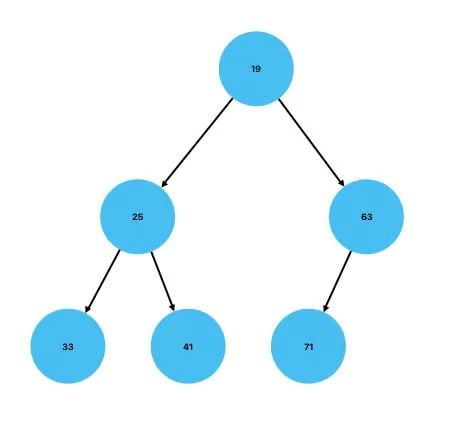
Here is the same heap represented as a tree:

The delete function can be implemented in JavaScript with the following code, taking advantage of heapifyDown() to bubble down the heap:

  delete() {
    if (this.length === 0) {
      return "The heap is empty";
    }

    const deletedValue = this.data[0];
    this.length--;

    if (this.length === 0) {
      this.data = [];
      return deletedValue;
    }

    this.data[0] = this.data[this.length];
    this.heapifyDown(0);
    return deletedValue;
  }

3 Use Cases for Heap

The following are some of the main uses of the heap data structure.

1. Heap Sort

A sorting algorithm that uses heaps as a data structure. This algorithm works by building a Max Heap, then using the delete() function to continuously move the largest value of the heap tail-end of the array. A heap sort can also be used for a Min Heap.

2. Priority Queue

A queue data structure where the element with the highest priority comes first. It shares all of the previously mentioned methods of a queue, with the only difference being that it is a Min or Max Heap.

3. Retrieval Tree (Trie)

Tries are search trees that are used to store a dynamic set of strings. They are useful for autocomplete and caching mechanisms.

More on Data ScienceHow to Heapify a Heap Tree in C++

Understanding the Heap Data Structure

Understanding what heaps are, how they work and how they may be implemented is vitally important when working with data structures and algorithms in computer programming. Hopefully this guide served as a useful introduction for anyone seeking a basic understanding of heaps.

Frequently Asked Questions

Is a heap a tree or an array?

A heap can be represented as both a tree and an array. Here is a visual representation of a Max Heap data structure as a tree:

 

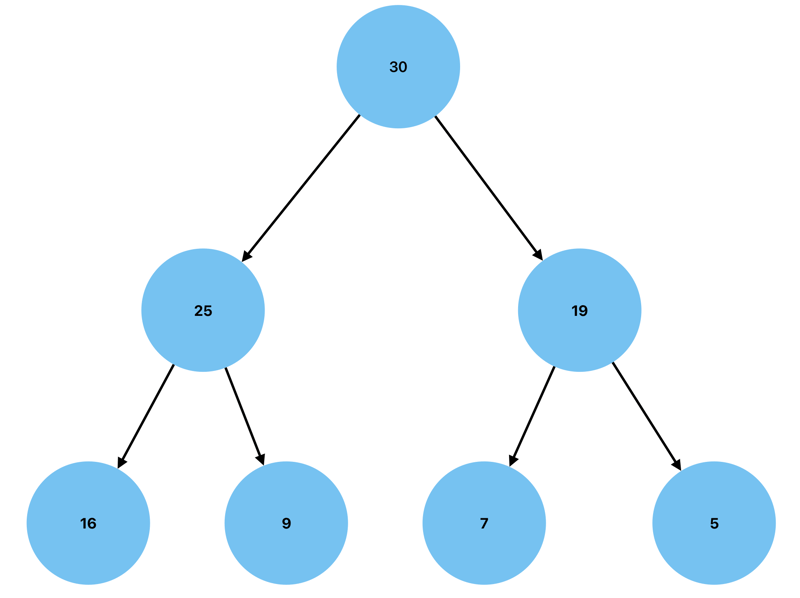
Here is that same Max Heap data structure as an array: